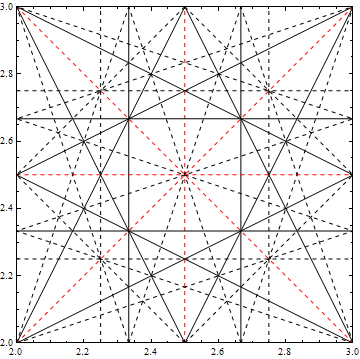
I am trying to move whatever I can to python. The main reason being that I want it to be free, and not require expensive commercial software. So recently I took the time to revisit my Mathematica code for the tune diagram and port it to Python. Basically I rewrote the whole thing and it has the nice feature that you can overlay it on top of whatever you want to plot.here you find my python code for plotting a resonance line diagram as the one found above.
The code should be self-explanatory, when you run the script directly with the option -o shows an example plot. When you import it, you can use the function plotTuneDiagram(maxOrder,xlim=[0,1],ylim=[0,1],tickOrders=False,tuneLineColor="black")
Parameters are
maxOrderthe maximum order of resonance line to be displayedxlim,ylimthe intervals in horizontal and vertical tune in which to plottickOrderswhether or not to place x- and y labels on full fractions up to selected ordertuneLineColorcolor for the tune lines, sensible when plotting on top of measurement or simulation data.